NEWS 活動経緯
- 【社是】Transforming Business with a Digital Engine 「デジタルエンジンでビジネスを変革する」
- 2020.10.1 商標【Digital Engine】・商願2020-121537
-
2020.8.13
【特許登録】特許第6749381号
「採寸値とデプス画像とを相互に生成するプログラム及び装置」 -
2019.6.18
【特許登録】特許第6719168号
「教師データとしてのデプス画像にラベルを付与するプログラム、装置及び方法」 - 2020.2.4 商標【3D×AI】・商願2020-011950
-
2020.2.28
【特許登録】特許第6667785号
「3次元モデルとデプス画像とを対応付けて学習するプログラム」 -
2019.1.9
特願2019-001566
「人体に基づくデプス画像と組成値とを対応付ける装置」 -
2018.10.26
【特許登録】特許第6424309号
「採寸値に基づく3次元モデルを生成するプログラム及び装置」
特許公報ダウンロード - * 商標登録「OrbisBrain」・登録第6127509号
TECHNOLOGIES 3D Sharing Engine / 3D Sharing Server
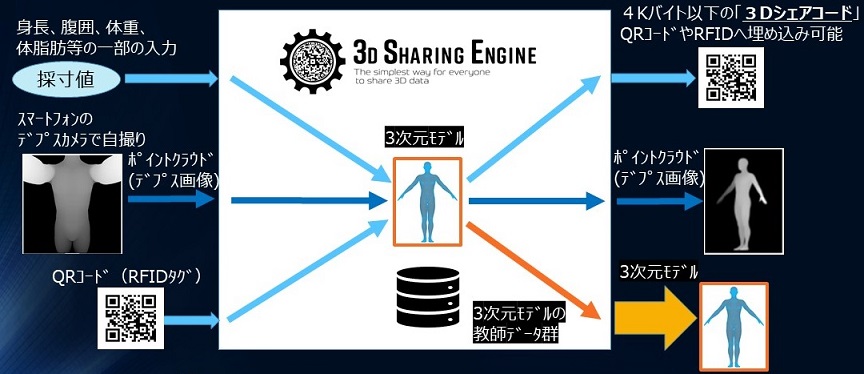
3Dシェアリングエンジン
3Dシェアリングエンジンは、人体の3次元モデルに基づく機械学習エンジンです。これは、「人体の3次元モデル」を介して、以下の3つの情報要素を、相互に交換することができます。
(1)個人情報としての体組成値(例えば身長、体重、体脂肪等)
(2)人体を所定視点から撮影したデプス(Depth)画像(2.5次元画像)
(3)QRコード、RDIFタグ、又は、クッキー情報
また、3Dシェアリングエンジンによれば、ユーザ自身の3次元モデルを、数カ所の体組成値(身長は必須、その他、体重、体脂肪など)だけで作成することができます。欠損した他の体組成値は推定され、そのユーザ自らの体型の3次元モデルを生成することができます。このとき、光学三角測量の3次元スキャナなどを用いる必要もありません。
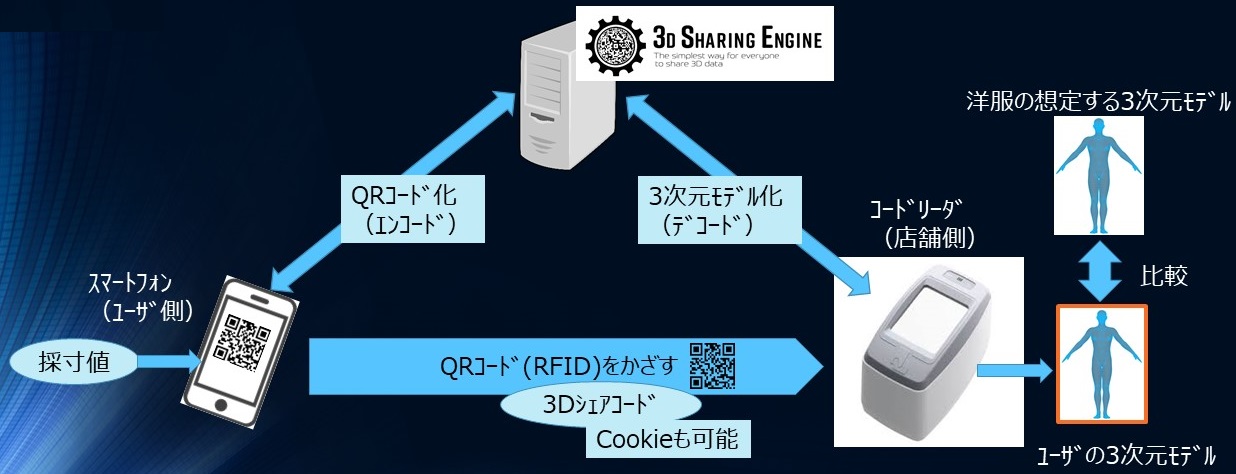
3Dシェアリングサーバ
3Dシェアリングエンジンは、サーバに搭載されており、ユーザ所持の端末や、事業者のサーバからアクセスすることできます。公開されたサーバインタフェースにアクセスするだけで、人体の3次元モデルのエンコード及びデコードを実現することができます。
TEAM メンバ紹介、Facebook
Member
取締役CTO 有光裕樹(Hiroki Arimitsu)
県立小倉高等学校・卒業・(吹奏楽部Tp.)
九州大学・工学部・エネルギー科学科・中退
2014~2017 フリーで、人体の3次元モデルに関する研究開発に従事
2018~現在 OrbisBrain創業準備
etc参照
代表取締役CEO 早原茂樹(Shigeki Hayahara)
弁理士・技術士(情報工学)
国立久留米工業高等専門学校・電気工学科・卒業・(ラグビー部)
電気通信大学大学院・電気通信学研究科・情報工学専攻・修了(修士)
1986~1996 沖電気工業株式会社・伝送端末の開発設計
1996~2005 国内特許事務所で内外国の特許業務
2005~現在 情報技術専攻・早原特許技術事務所・所長
2018~現在 OrbisBrain創業準備
https://www.hayahara.com
COMPANY 会社情報
| 会社名 | 株式会社OrbisBrain (2019年5月23日・法人設立) |
|---|---|
| 代表取締役CEO | 早原 茂樹・co-founder |
| 取締役CTO | 有光 裕樹・co-founder |
| 住所 | 〒802-0001 福岡県北九州市小倉北区浅野3-8-1 AIMビル6F コンパス小倉内 |
| 連絡先 | hayahara@orbisbrain.com |
etc 有光裕樹の過去の研究活動(2014~2017)
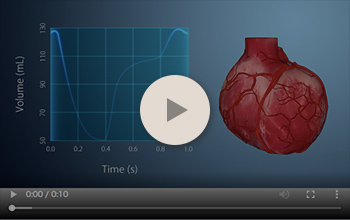
体積計算
この動画は、心室の容積データと同期して、心臓が拍動する様子を表しています。 従来、ポリゴンメッシュの体積計算の多くは、物理演算によって実現されており、計算負荷の高いものでした。そのため、Unity等のリアルタイムエンジン上で、物体の体積を維持した変形を行うことは困難でした。
そこで、リアルタイム用途を想定した、物理演算に依らない体積計算アルゴリズムを開発しました。 このアルゴリズムは、ポリゴンメッシュの変形に応じて、初期状態の体積を強制して変形させます。 ポリゴンメッシュの収縮に対して膨張し、膨張に対して収縮し、適切な体積を維持し続けます。数値入力やグラフの波形から、体積の変化を手動で制御することもできます。
また、ポリゴンメッシュは多角形の集合で構成されているので、通常は厚みを持ちません。 そこで、動画の例では、二重構造のポリゴンメッシュにより、皮膚や筋組織の厚みを再現しています。 動画では、心筋が収縮するにつれて、筋組織は厚みを増し、同時に心室内の容積は適切に保たれています。また医療データから、リアルタイムに心臓の拍動をシミュレーションしています。
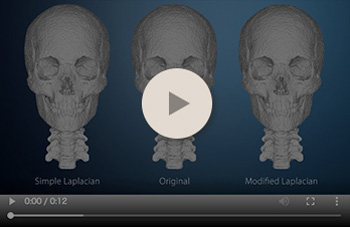
メッシュスムージング
この動画は、ノイズの多い三次元モデルデータのスムージング処理を表しています。 これは、ポリゴンメッシュ上の各頂点を、その頂点と周囲の頂点との重心方向に移動するように操作します。 この操作を繰り返すことにより、各頂点は周囲の頂点と平均化され、結果的に凹凸のない滑らかなポリゴンメッシュが得られます。 しかし、一般的な凸状の多面体の場合、頂点座標の平均化は各頂点を凹方向に移動する操作となり、ポリゴンメッシュ全体が収縮してしまいます。 動画左では、骨表面が滑らかになるにつれて、それぞれの骨が収縮していく様子が分かります。
これに対し、動画右では、収縮性の平均化と膨張性の平均化を並行させることで、この問題を解決しています。 各頂点を周囲の頂点と平均化することによって、近傍の凹凸のみが平均化され、ポリゴンメッシュ全体が収縮していません。 これによって、ノイズを効果的に減らしながら、本来のモデル形状を損なわないスムージング処理を行うことができます。
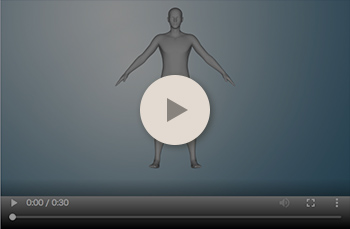
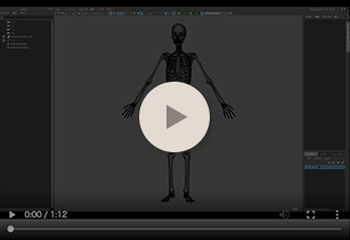
骨格推定
この動画は、任意の体型の人体モデルに対して、体内の骨格構造を推定する処理を示しています。 ポリゴンメッシュ表面の変形に応じて、内部ポリゴンメッシュを変形させる手法としては、「ケージ変形」が一般的です。 ケージ変形は、ポリゴンメッシュ表面を内部を囲う枠(ケージ)として扱い、枠内の構造を維持します。 しかしながら、計算負荷が高くなると共に、純粋に幾何学的な変形であるために解剖学的な構造を反映しません。
動画では、スキニング変形とその逆演算から、骨格構造を推定しています。 スキニング変形とは、擬似的な骨格構造とその関節の変位に基づいて、ポリゴンメッシュを変形させる手法です。 まず、ベース人体モデルと骨格モデルとに、解剖学的な構造を考慮したスキニング変形を適用します。 そして、ベース人体モデルと、与えられた人体モデルから得られる関節の変位を骨格モデルに適用します。
これによって、骨格構造を、高速な計算で推定することができます。 また、汎用性の高いスキニング変形を用いるために、ベース人体モデルの開発に注力しさえすれば、任意の人体モデルに対して汎用的に再利用できます。 尚、動画では骨格系の推定のみですが、勿論、筋肉も含めた筋骨格系やその他の器官系(循環器系、神経系、消化器系、呼吸器系等)にも応用することができます。
解剖学に即した筋骨格系のリギングアプローチ
筋骨格系の基本的なリギングアプローチは、骨格を構成する関節位置にジョイント(計算機上の関節)を配置し、 ジョイントを中心にポリゴンメッシュを回転させるというものです。 従来のリギングモデルは、非常に単純化した骨格モデルに基づいており、人体の運動を表現する上で十分な機能を備えていませんでした。 例えば、単関節(2つの骨からなる関節)ではなく複関節(3つ以上の骨からなる関節)である肘関節は、多くの場合、単一のジョイントによる回転で近似されます。 また、脊柱は、約30個の椎骨がS字状に湾曲しながら連結したものですが、回転に使用されるジョイントの数は5つ程度です。
前述の骨格推定の動画では、従来どおり、骨格とジョイントとを対応付けることによって、筋骨格系のリギングを行っています。
骨格のリギングでは、解剖学に即した関節位置にジョイントを配置し、解剖学上の運動表現(屈曲、伸展、外転、内転、回旋、外旋、内旋、回外、回内、側屈等)に基づいて、ジョイントの回転を制御します。
筋肉のリギングでは、まず筋肉と骨格とを対応付け、それによって、筋肉とジョイントとの対応を決定します。
本来、まず筋肉の収縮が起こり、それが骨を回転させますが、その反対のモデルを考えることで、筋肉と骨格を対応付けます。
前腕回転
この動画は、前腕の回内・回外の様子を表しています。 従来の前腕の回転計算は、ジョイントを肘関節に1つ配置し、肘ジョイントを中心にポリゴンメッシュを回転させて実現していました。 この方法では、肘の屈曲は表現できても、回内・回外(ジョイントの捻り)を適切に行えないという問題がありました。 肘と手首の間にもう1つの補助ジョイントを配置し、2段階で捻りを表現する手法もあります。 そこで、解剖学的な観点から2つのジョイントを配置し、それによって前腕のポリゴンメッシュを回転させる手法を取りました。 まず、前腕の回内・回外を行う2つの骨(尺骨と橈骨)と上腕骨との関節位置に、ジョイントを2つ配置します。 腕尺関節は蝶番関節であり、腕橈関節は球関節であるので、回内・回外の動作は、橈骨が尺骨を跨ぐことによって起こります。 尺骨ジョイント・橈骨ジョイントの回転は、この動作を模倣するように決定します。
前腕筋群の回転は、それぞれが尺骨ジョイント・橈骨ジョイントの影響をどの程度受けるかで決定します。 実際には、まず筋肉の収縮が起こり、それが骨を回転させますが、ここでは反対に、骨に筋肉を追従させます。 肘と手首を通る直線に垂直な平面状で、前腕筋群と尺骨・橈骨との距離を計算し、距離の比から適切に重み付けしています。
これによって、動画のように、解剖学的に、より正確に前腕を変形させることができます。
3DCGモデルセット
これは、詳細かつ解剖学的に正確な人間の皮膚、筋膜、筋肉および骨格系を含むモデルセットです。 芸術的な外観になるように設計されていますが、3D空間での筋肉や肌のシミュレーションにも高度に最適化されています。 また、非常に複雑で密な構造ですが、交差点や自己交差点はまったくありません。 更に、各フェースは、リラックスした均一なサイズとグリッド状のトポロジで構成されています。 これにより、バイアスのない信頼性の高いシミュレーション結果が得られます。 この安定性は、望ましくない結果や予期しないエラーでシミュレーションを繰り返す回数を減らし、品質にもっと集中することができます。
使い方はとても簡単です。 モデルのスキンシェイプとこのモデルのスキンシェイプの両方に一致します。使い方はとても簡単です。 次にシミュレートします。これで十分です。 形状に合わせるには2つの方法があります。 モデルをこのモデルにマッチさせると、シュリンクラップが最適です。 より正確な結果を得るための高解像度スキンモデルと、より便利な操作のための低解像度スキンモデルが含まれています。 このモデルをモデルにマッチさせる場合は、ケージ変形を使用するか、個別にマッスルをスカルプトしてモデルのスキンに合わせることができます。 それでも、シミュレーションの開始フレームでの筋肉の形状は、彫刻のないデフォルトの状態であることが推奨されます。 交差点や自己交差点は注意深く削除されているため、通常は布シミュレーションで行われるように、シミュレーションは常に初期状態から開始する必要があります。 また、シミュレーションを実行する際に腱を修正するためのウェイトマップも用意されています。 MayaユーザでnClothを使用している場合は、このウェイトマップをnClothのinputMeshAttract属性に適用してください。 それは筋肉に沿って均一で美しい流れで構成されたモデルでもあり、彫刻のための理想的なベースメッシュです。 スキンの形状は実際にはこの筋肉モデルのシミュレーションの結果であり、ほとんど追加の彫刻は行われません。 これは、皮膚の形状も解剖学的に信頼できることを意味します。
DeltaMush
DeltaMushは、Rhythm & Hues Studiosによって開発されたポリゴンメッシュの変形アルゴリズム(※デフォーマ)です。 ポリゴンメッシュの平滑化により、デフォーメーションアーティファクトを軽減するとともに、平滑化により失われたディテールを復元します。 あらゆるデフォメーションアーティファクトに対し、堅牢なアルゴリズムです。
(1)対象ポリゴンメッシュと参照ポリゴンメッシュを平滑化する (2)参照ポリゴンメッシュの各頂点に対して平滑化前後の差分ベクトルを得る (3)対象ポリゴンメッシュと参照ポリゴンメッシュの対応する頂点とその一近傍頂点を評価し、接線空間の回転変換を得る (4)参照ポリゴンメッシュの平滑化差分ベクトルを回転変換し、対象ポリゴンメッシュに差分を適用する ポリゴンメッシュの平滑化 : LaplacianSmoothing